Online-Rechner zur Bestimmung der Zugmasse von Modellbahnwagen (Java-Script notwendig)

In der Modellbahn spielt beim Anlagenbetrieb stets die Zugkraft von Lokomotiven eine Rolle. Unglücklicherweise wird diese Zugkraft in Publikationen nicht in Newton (die Einheit einer Kraft), sondern physikalisch falsch, in Gramm (Einheit einer Masse) angegeben. Daher sind zuerst ein paar Definitionen notwendig, damit im Folgenden von Zugmassen die Rede sein kann:

Im Gegensatz zu den leicht zugänglichen Zugmassen der angetriebenen Modelle sind die Zugmassen, die zum Bewegen der Wagen benötigt werden meistens unbekannt und werden gerne ignoriert. Dabei ist die Bestimmung der Zugmassen von Wagen sehr einfach. Die theoretische und praktische Betrachtung soll daher an dieser Stelle folgen.

Theorie


Alles rollende Material hat einen Fahrwiderstand, welcher von der Eigenmasse, den Streckenverhältnissen (Steigungen, Kurven) und der Konstruktion (Radmaterial) abhängt. Man kann daher einen Ansatz folgender Art machen:
Ffahr = (μroll+μSteig+μreib+μKurv+μLuft)*Fges+μSchleifer*Fges

Da die Kräfte den selben Faktor g aus F = mg haben, kann man diesen wegkürzen und man erhält die Massengleichung:
mfahr = (μroll+μSteig+μreib+μKurv+μLuft)*mges+μSchleifer*mges

Dabei haben die Faktoren folgende Bedeutung:
μroll rollende Reibung
μSteig Steigung
μreib Lagerreibung
μKurv Kurvenwiderstand
μLuft Luftwiderstand
μSchleifer Schleiferwiderstand
Alle diese Faktoren sind aus mechanischen Größen mindestens abschätzbar. Daher sollen die Faktoren der Reihe nach besprochen werden.

μLuft
Der Luftwiderstand spielt nur bei hohen Geschwindigkeiten eine Rolle und berechnet sich nach:

μLuft=(ρ/2)*A*cw*v2/(mg)
ρ ist die Luftdichte (1,293 kg/m3), A ist die Querschnittsfläche, die von der Luft umspült wird (in m2), cw ist der experimentell zugägliche Luftwiderstandskoeffizient (ohne Einheit) und v ist die Geschwindigkeit in m/s. In der Modellbahn spielt dieser Faktor keine Rolle. Beispiel: A einer Wagenstirnwand ist ca. 4cm2, cw ca. 0,1 und v ist < 1m/s. Folglich ergibt sich für einen Wagen mit m=100g Masse ein μLuft von 2,7*10-5 oder 0,0027%. Gemessen an den folgenden Koeffizienten im Prozentbereich drei Größenordnungen kleiner.

μSchleifer
Wagen mit Schleifer haben einen bisweilen deutlich größeren Fahrwiderstand aufgrund der Feststoffreibung des Schleifers am Mittelleiter. Dieser zusätzliche Widerstand ist experimentell zugänglich, indem die Andrückkraft des Schleifers auf die Gesamtmasse bezogen wird:

μSchleifer = FSchleifer/Fges

Die Verwendung eines Koeffizienten ist physikalisch nicht korrekt, sie wird jedoch wegen der Zweckmäßigkeit hier angewandt. Bisher überprüft:

Diese überschlagsmäßig gemessenen Kräfte sind mit 0.17 (Gleitreibung Metall-Metall) zu multiplizieren um die wirksame Kraft zu erhalten.

μSteig
Die Steigung einer Strecke wird stets in % angegeben und kann daher direkt übernommen werden. Möglich sind Steigungen bis ca. 7% für vorbildgerechte Anlagen und bis zu 15% in Modellbahnanlagen bei beengten Platzverhältnissen. Als Koeffizient entspricht 1% dem Faktor 0,01.

μroll
Für die rollende Reibung gibt es folgenden Ansatz:
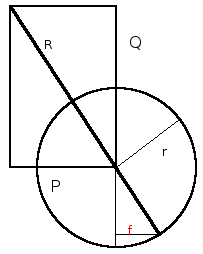Die senkrecht zur Gewichtskraft der Wagenmasse Q (ohne Radsätze) steht die aufzubringende Reibkraft P. Beide stehen im Verhältnis

P = μreibQ

. Vektoraddition beider Kräfte ergibt die Resultierende R, die im Winkel arctan (Q/P) zu Q steht. Verlängert man diese Resultierende R bis zum Radradius r ergibt sich der Hebelarm der rollenden Reibung f zu r*sin(arctan(P/Q)) oder
f = sin(arctan(μreib)) * r

Befindet sich diese Achse mit dem Radius r in einem Rad mit dem Radius RRad, so verkleinert sich nach dem Hebelgesetz die notwendige Kraft auf das r/R-fache. Zugleich kommt noch die zur Rollbewegung notwendige Kraft für die Radsätze hinzu, und man erhält:
mroll=(f/Rrad)*(Q+mradsatz) = sin(arctan(μreib))*(r/RRad)*mges

Daraus berechnet sich der Koeffizient für die rollende Reibung nach

μroll = mRoll/(mges) = sin(arctan(μreib))*(r/RRad)

μreib
Im Achslager werden die für eine reine Flüssigreibung notwendigen Drehzahlen nicht erreicht und es bleibt eine Gleitreibung übrig. Deren Größe hängt nur von der Wagenmasse (ohne Räder) und dem Zustand im Achslager ab. Diese Reibkraft wird ebenfalls nach dem Hebelgesetz, diesmal mit r/RRad auf die Schienen übertragen. Folglich setzt man an:

μreib= μLager * (mWagen/mges) * (r/RRad)

μkurv

Herleitung des Kurvenwiderstands ohne Radabstand auf der Achse

Zur Berücksichtigung des Radabstands auf der Achse hier klicken


 

Der spezifische Fahrwiderstand setzt sich nun additiv aus allen Koeffizienten zusammen:
wt,rel = μroll+μSteig+μreib+μKurv+μLuft+μSchleifer

Man erhält schließlich die benötigte Zugmasse nach :

mZug = wt,rel * mges

und folglich auch die Zugkraft gemäß :

FZug = mZug*g

In der folgenden Tabelle können Sie nun die einzelnen Angaben nutzen, um die Zugmasse für ein bestimmtes Wagenmodell zu berechnen: (Kommazahlen bitte mit Punkt eingeben!)

Wagenmasse in gRollwiderstandSteigung LagerreibungswiderstandKurvenwiderstandSchleiferwiderstandErgebnis

Radius im Achslager in mm:
Laufkreisradius in mm: 		o/oo
Wagenmasse ohne Räder in g: 		 
Achstand: mm
Spurweite:
Spurkranzhöhe: mm
Schienenradius: mm 		FZug: mN
mZug: g
wt,rel: %

Anteil am
Gesamtwiderstand		   mN
  g
  %		   mN
  g
  %		   mN
  g
  %		   mN
  g
  %  		   mN
  g
  %		  

Schrifttum

F. Sass, Ch. Bouche, A. Leitner, "Dubbel's Taschenbuch für den Maschinenbau", 12. Auflage 1963, Springer-Verlag ohG, Berlin/Göttingen/Heidelberg

Karl-Heinrich Grote, Jörg Feldhusen, "Dubbel Taschenbuch für den Maschinenbau" 21. Auflage 2005, Springer-Verlag Berlin, Heidelberg, New York, ISBN 3-540-22142-5

10349 Besucher seit dem 19.04.2005
Falls Sie Anregungen oder Kritik haben, schreiben Sie mir.